Computational Materials Science: Understanding materials from the atomic to the macroscopic scale
- Lokesh Verma

- Mar 20, 2020
- 4 min read
Materials science is an interdisciplinary field concerned with the understanding and application of the properties of matter. It is used to study the relations between the underlying structure of a material, its properties, its processing methods and its performance in applications. In simple words, materials science teaches us what things are made of and why they behave as they do. Materials science was for long considered as a sub-field of analytical physics, chemistry and engineering, however, in the 1940s, it began to be more widely recognized as a specific and distinct field of science and engineering. Since then it has found applications in engineering domains such as electronics, aerospace, tele-communications, information processing, nuclear power, energy conversion, among others.
The conventional approach to understand materials is via experimental measurements. Generally speaking, experimental measurement, which usually deals with microstructure and property analysis, property measurement, and so on, is an easy and intuitive method of materials research, however, it is usually carried out in an inefficient manner over a long time period. Moreover, this kind of approach poses high requirements in terms of the equipment, the experimental environment, and the expertise of the researcher.
Another approach to exploit the existing theory for analysis of materials is via the computational simulations using computer programs. This field of study is called Computational Materials Science. Compared with experimental measurements, computational simulations require less time and are advantageous for supplying real experiments in that one has full control over the relevant variables. The main goals of computational material science include discovering new materials, determining material behaviour and mechanisms, explaining experiments, and exploring materials theories. Computational materials science has evolved into a predictive tool for allowing the explanation of the properties and behaviour of materials.
Depending on their spatial and temporal scales, modelling of computational materials falls primarily into four categories: electronic, atomistic, mesoscopic and continuum (Fig.1).
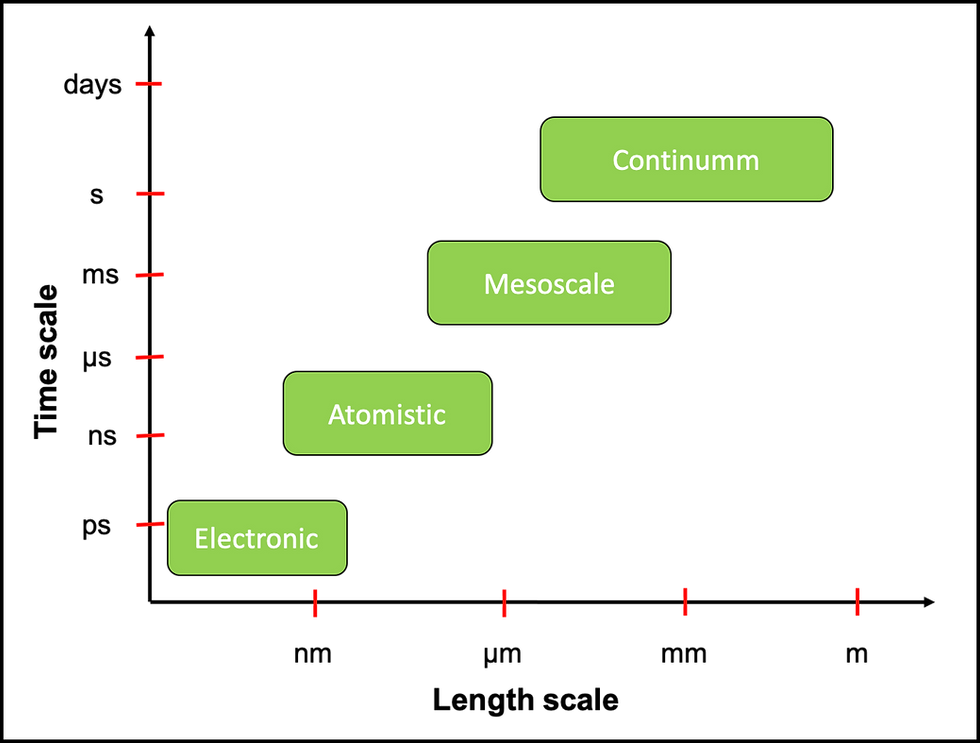
Fig.1: Length and time scales for studying materials.
The capability to communicate between these length and time scales plays a key role in predicting material properties and behaviour. There exist different mathematical models for investigating problems at different length and time scales. Each method/model can be used as a stand-alone model to predict materials properties and mechanisms, to provide information to other simulation methods, or to directly compare with experiment. Some of the computational methods available at the different scales include:
Electronic structure calculations
Electronic structure methods solve the Schrödinger equation to calculate the energy of a system of electrons and atoms. The length scales range up to the nanometer (nm) regime and the time scales lie in the picosecond (ps) regime. The most popular computational method in this domain is the Density Functional Theory (DFT). Some areas of research using the electronic structure calculations include charge transport in nanoscale wires for future electronic devices and design of electrochemical interfaces for energy conversion and new functional perovskite materials.
Atomistic models
The length scales in this domain range from 1 to 10 nm and the time scales lie in the nanosecond (ns) regime. Molecular Dynamics (MD), Accelerated Molecular Dynamics and Monte Carlo (MC) methods are considered as preferred tools in the atomistic domain. Molecular Dynamics study can be used, for example, for the design of nanostructured materials for energy applications, mass and thermal transport, dynamics of molecular motors, etc.
Meso-scale models
The length scales range from 100 to 1000 nm and the time scales range up to few microseconds (ms) in the meso-scale domain. The most common models to deal with such length scales (between micro and nano) include the Phase-field, kinetic Monte Carlo (kMC), Cluster Dynamics and Dislocation Dynamics (DD) methods. Examples of applications using the meso-scale models include simulating the properties of materials, including microstructural evolution, solidification, grain growth and electrochemical transport.
Continuum models
The continuum scale modelling can stretch to several days in terms of the time scale and to centimeters (cm) for the length scale depending on the problem. Finite Element Method (FEM) is most useful computational technique for materials related calculation at the continuum scale level. An example of FEM application can be the detailed visualization of where structures bend or twist, and indication of the distribution of stresses and displacements in structures.
Various available models and methods operating in the different length and time regimes are depicted in Fig.2.
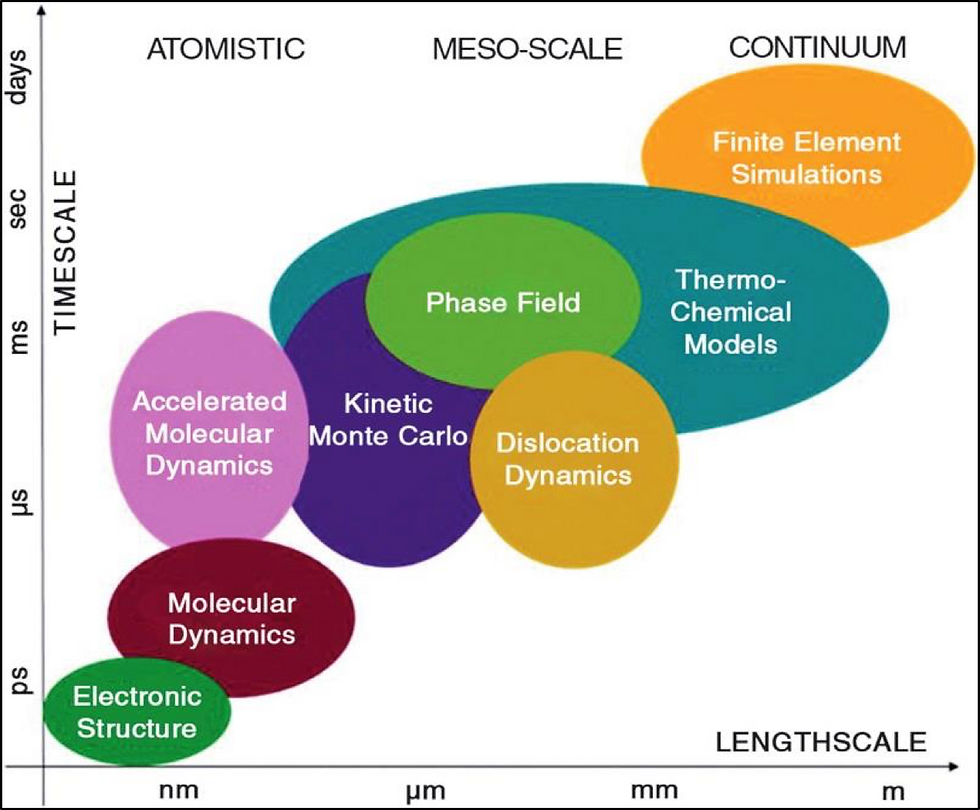
Fig.2: Computational models available in the different scales [1].
Experimental and computational data are needed to validate codes and for model development. Computational materials modelling also goes hand-in-hand with High Performance Computing (HPC). With the recent progress in available computational power, predictive materials modelling seems promising to enable economic advantages for all manufacturing industries. There are ongoing researches to further enhance the computational modelling capabilities.
Several material problems exist which have important features at multiple length scales. Multiscale modelling approach is often used for such problems. It involves exchange of information between computational tools at different length scales. Multiscale modelling is one such approach that is gaining momentum in the research community in recent years and will allow us to better utilize computational materials modelling to understand materials behaviour.
[1] M. Stan. Discovery and design of nuclear fuels. Materials Today, 12(11):20–28, 2009.





Comments